Skip to main content

Analisis Regresi Menggunakan R

1 Pendahuluan

Di era teknologi dan informasi yang overload seperti sekarang, kita kadang tertarik untuk melakukan investigasi tentang hubungan antara suatu variabel dengan variabel lain. Tertulis atau hanya tercatat di dalam pikiran, di dalam proses investigasi ini, kita menyusun hipotesis-hipotesis tentang hubungan antar variabel-variabel yang menjadi perhatian kita.

Untuk sampai pada kesimpulan mengenai hubungan-hubungan yang kita buat, kita merancang investigasinya, mengumpulkan data-data kemudian menganalisisnya. Di dalam proses analisis ini, seorang investigator biasanya menggunakan data sampel yang berasal dari suatu populasi. Hasil analisisnya dapat menyediakan bukti-bukti statistik yang mendukung atau menolak hipotesis yang telah dibuat serta menampilkan karakteristik-karakteristik penting dari populasi dimana data yang dianalisis berasal.

Proses investigasi ini biasanya iteratif, tidak sekali luncur langsung selesai. Dalam beberapa hal, investigasi harus kita ulang lagi sampai didapatkan sebuah model statistik yang memuaskan dengan mempertimbangkan kepraktisan, biaya dan waktu yang tersedia.

Subjek investigasi atau percobaan kita dapat berupa hal-hal yang berada di dalam atau di luar diri kita, yang kasatmata atau tidak. Aerobiologi mempelajari partikel-partikel organik (bakteri, spora jamur, polen, serangga-serangga kecil) yang terbawa udara secara pasif. Astronomi mempelajari benda langit dan fenomena-fenomena alam yang terjadi di luar atmosfer bumi. Ilmu Ekonomi mempelajari kegiatan produksi, alokasi dan distribusi barang dan jasa. Psikologi mempelajari alam pikiran manusia. Geologi mempelajari bentuk dan komposisi bumi.

Analisis regresi tidak mempelajari suatu subjek secara langsung tetapi sebagai alat analisis yang dipakai di sebuah bidang ilmu. Kegunaannya tidak langsung tetapi melalui bantuan yang diberikan ke bidang ilmu lain.

Analisis regresi sangat berguna, sebab hampir semua cabang ilmu pengetahuan harus berhubungan dengan data yang tidak sempurna. Ketidaksempurnaan data ini mungkin terjadi karena kita hanya dapat mengamati dan mencatat sebagian saja dari apa yang relevan dengan subjek penelitian kita.

Atau bisa juga karena kita hanya dapat mengamati secara tidak langsung dari apa yang benar-benar relevan dengan subjek yang diamati. Mungkin juga karena seberapapun hati-hati kita melakukan observasi atau mendesain sebuah percobaan, data yang diperoleh akan selalu mengandung unsur ‘gangguan’ (noise).

Analisis regresi adalah salah satu teknik statistik yang paling luas dipakai (Agresti, 2015; Cheng-Few Lee, 2013; Frees, 2016). Penerapannya meliputi hampir semua bidang ilmu: bisnis, ekonomi, teknik, ilmu-ilmu sosial, biologi dan kesehatan. Pada beberapa proyek penelitian analisis regresi bahkan seringkali menjadi alat analisis utamanya. Keberhasilan penerapan model regresi linier memerlukan pemahaman baik akan teori yang mendasarinya maupun persoalan-persoalan praktis yang sering terjadi di dalam penggunaan alat analisis ini dalam situasi riil.

1.1 Model Regresi Linier

Model di dalam analisis regresi merujuk pada ekspresi matematik yang menjelaskan perilaku-perilaku dari variabel-variabel yang menjadi perhatian. Model regresi linier atau biasa disebut analisis regresi (Faraway, 2014) digunakan untuk menjelaskan atau memodelkan hubungan antara satu variabel respons \(y\) dengan satu atau lebih variabel prediktor \(x_1, x_2, ... , x_p\), dimana \(p\) adalah jumlah prediktor. Secara khusus, analisis regresi adalah upaya untuk menjelaskan pergerakan sebuah variabel respons dengan merujuk pada pergerakan satu atau lebih variabel eksplanatori. Jika \(p=1\), modelnya disebut regresi sederhana. Tetapi jika \(p>1\), disebut regresi berganda.

Dalam analisis regresi, kita dapat menggunakan pengetahuan tentang hubungan ini untuk memprediksi respons variabel \(y\) melalui variabel \(x\). Karena hubungan inilah maka \(y\) disebut variabel respons dan \(x\) disebut variabel prediktor. Rumpun ilmu berbeda kadang menggunakan istilah yang berbeda untuk menyebut variabel \(x\) dan \(y\), seperti yang ditunjukkan pada Tabel berikut.

Di dalam ekonometrika seringkali digunakan istilah variabel dependen dan variabel independen. Di bidang ilmu yang berhubungan dengan eksperimen biasanya digunakan istilah variabel respons dan variabel kontrol karena variabel \(x\) berada dibawah kendali peneliti. Dibuku ini penyebutan-penyebutan itu akan digunakan secara bebas.

Tabel 1.1: Berbagai Penyebutan Variabel
Variabel y Variabel x
Dependen Independen
Endogen Eksogen
Respons Perlakuan/Kontrol
Regressand Regressor
Ruas kiri persamaan Ruas kanan persamaan
Diprediksi Prediktor
Output Input
Dijelaskan Penjelas/Eksplanatori

Jika memungkinkan, di dalam analisis regresi kita juga ingin menyimpulkan apakah terdapat hubungan sebab-akibat: mengetahui pengaruh dari variabel prediktor terhadap variabel respons.

Beberapa contoh kasus analisis regresi misalnya:

  1. Hubungan antara ukuran kelas/jumlah siswa per kelas dengan rata-rata nilai pelajaran Bahasa Daerah di sebuah SMA. Disini \(y\) adalah rata-rata nilai pelajaran Bahasa Daerah dan \(x\) adalah jumlah siswa per kelas.
  2. Hubungan antara tingkat pendapatan seseorang (\(y\)) dengan pendidikan terakhir yang ditamatkannya (\(x\)).
  3. Kinerja karyawan dapat diprediksi dengan menggunakan hubungan antara kinerja (\(y\)) dan hasil tes aptitutenya (\(x\)).
  4. Apakah terdapat hubungan antara tingkat kelahiran penduduk suatu negara dengan tingkat pendapatan perkapitanya? Jika diperhatikan negara-negara dengan tingkat pendapatan per kapita tinggi (\(x\)), tingkat pertumbuhan penduduknya rendah (\(y\)), dan sebaliknya.
  5. Jumlah kosakata seorang anak dapat diprediksi dengan menggunakan pengetahuan hubungan antara jumlah kosa kata (\(y\)), usia anak (\(x_1\)) dan tingkat pendidikan orang tua si anak (\(x_2\)).
  6. Hubungan antara desain pekerjaan (\(x\)) dengan perilaku karyawan di sebuah perusahaan (\(y\)). Perusahaan menginginkan agar karyawan beraktivitas dan berinteraksi secara efektif sehingga pekerjaan harus didesain dengan baik sehingga menghasilkan perilaku positif dan komitmen tinggi karyawan terhadap pekerjaannya. Walaupun inti investigasi ini adalah analisis regresi, tetapi di dalam contoh ini, kita berhubungan dengan konsep-konsep abstrak/konstruk-konstruk yang memerlukan alat analisis sendiri seperti analisis faktor. Topik ini dibahas di buku saya yang lain tentang analisis faktor.

Sebagai ilustrasi, kita akan menggunakan kasus hubungan antara tingkat penjualan sepeda motor dengan pertumbuhan pendapatan per kapita di Indonesia dalam 20 tahun terakhir. Motor sebagai salah satu moda transportasi sangat populer di Indonesia karena berbagai alasan: praktis dan terjangkau. Penjualan motor berhubungan dengan tingkat pendapatan, harga motor, ketersediaan moda transportasi alternatif, selera, dll. Di kasus ini kita hanya mengambil pendapatan sebagai variabel eksplanatori.

Tabel berikut menunjukkan data dalam kasus ini. Data penjualan motor (\(y\)) diperoleh dari AISI, sedangkan data pendapatan didekati dengan pertumbuhan pendapatan per kapita (\(x\)) yang diperoleh dari World Bank. Satuan \(y\) dalam juta unit, sedangkan \(x\) dalam persen. Secara teoritis terdapat hubungan positif antara tingkat pendapatan dengan penjualan motor karena motor adalah barang normal.

Tabel 1.2: Penjualan Motor dan Pertumbuhan Pendapatan Per Kapita
Tahun y x
2001 1.58 2.24
2002 2.29 3.09
2003 2.81 3.38
2004 3.89 3.63
2005 5.07 4.29
2006 4.43 4.11
2007 4.69 4.95
2008 6.22 4.62
2009 5.95 3.25
2010 7.37 4.81
Tahun y x
2011 8.01 4.75
2012 7.06 4.61
2013 7.74 4.15
2014 7.87 3.64
2015 6.48 3.56
2016 5.93 3.76
2017 5.89 3.84
2018 6.38 3.99
2019 6.49 3.87

Langkah awal untuk melihat apakah memang terdapat “sinyal” yang menunjukkan hubungan antara pendapatan dengan penjualan motor dari data yang kita miliki adalah dengan mengamati data secara berpasangan dan membuat diagram pencarnya (scatter plot/scatter diagram). Setiap data \(y\) dipasangkan dan diplot terhadap nilai \(x\)-nya.

Diagram pencar bisa menunjukkan secara kasar apakah hubungan antar variabel dapat dianggap linier atau tidak. Jika nilai \(y\) cenderung meningkat atau menurun secara garis lurus ketika nilai \(x\) meningkat, dan jika perpencaran pasangan titik-titik (\(x,y\)) berada disekitar garis lurus, maka kita dapat menjelaskan hubungan antara \(y\) dan \(x\) dengan menggunakan model regresi linier. Hasil plot pada Gambar 1.1 menunjukkan bahwa memang terdapat sinyal yang sesuai dengan asumsi yaitu penjualan motor proporsional dengan pertumbuhan pendapatan per kapita: semakin tinggi pertumbuhan pendapatan per kapita semakin tinggi pula tingkat penjualan motor.

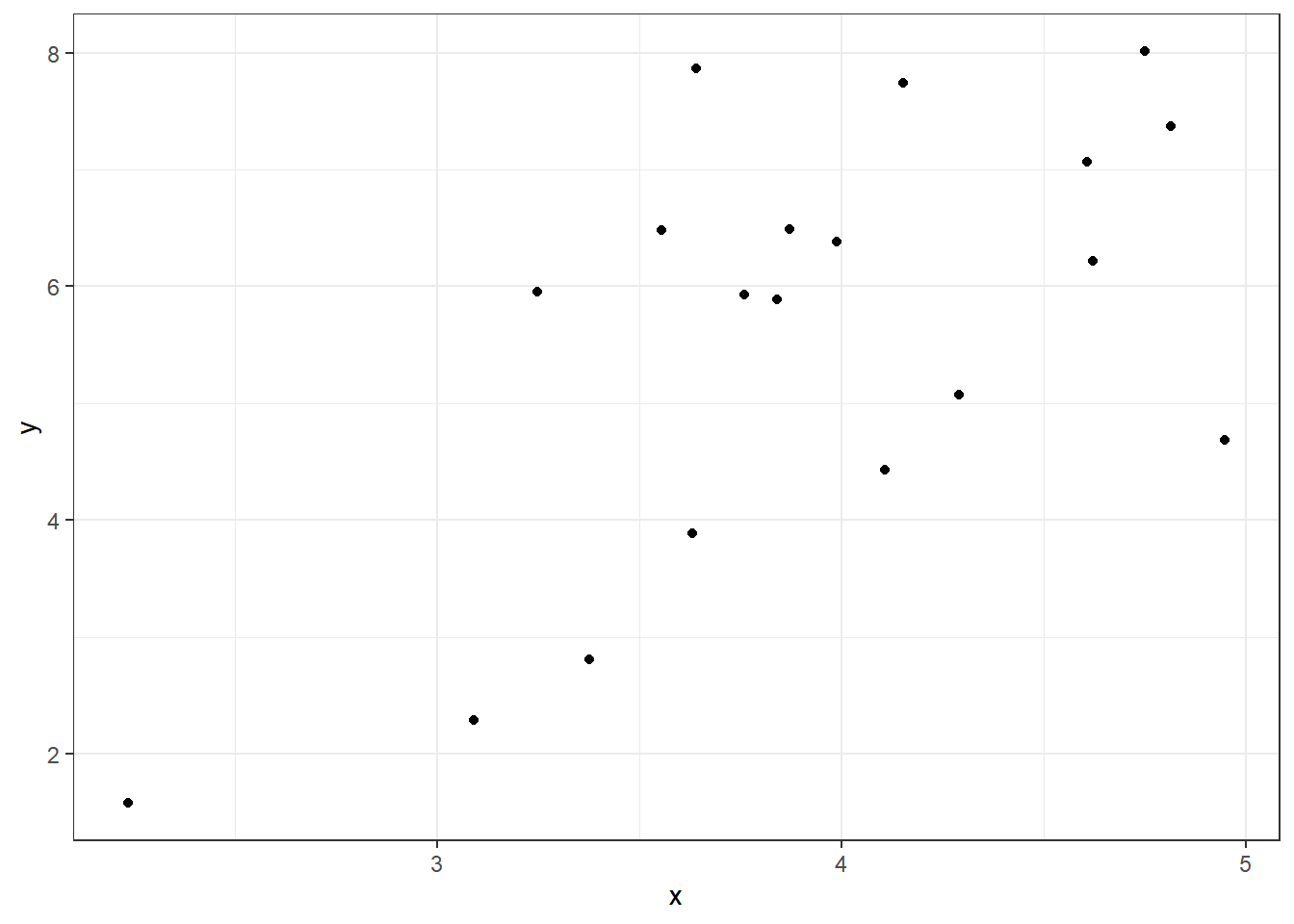
Diagram Pencar Penjualan Motor (y) sebagai Fungsi dari Pendapatan per Kapita (x)

Gambar 1.1: Diagram Pencar Penjualan Motor (y) sebagai Fungsi dari Pendapatan per Kapita (x)

Selanjutnya kita tambahkan sebuah garis lurus yang paling banyak “mendekati” titik-titik data pengamatan yang tersebar. Sebuah garis lurus yang kita tarik seperti pada Gambar 1.2 menunjukkan bahwa proporsionalitas ini memang ada tetapi tidak ketat. Garis lurus yang kita tambahkan tidak menyinggung seluruh data yang tersebar. Dengan kata lain data sampel tidak bisa seluruhnya tepat berada pada garis yang dibuat. Titik-titik pengamatan ada yang tepat digaris, ada juga yang di atas atau di bawah garis.

Ini menunjukkan adanya variasi pada penjualan motor yang tidak berhubungan dengan tingkat pendapatan. Atau terdapat faktor-faktor lain selain pendapatan yang juga mempengaruhi tingkat penjualan tetapi tidak tercakup di dalam model.

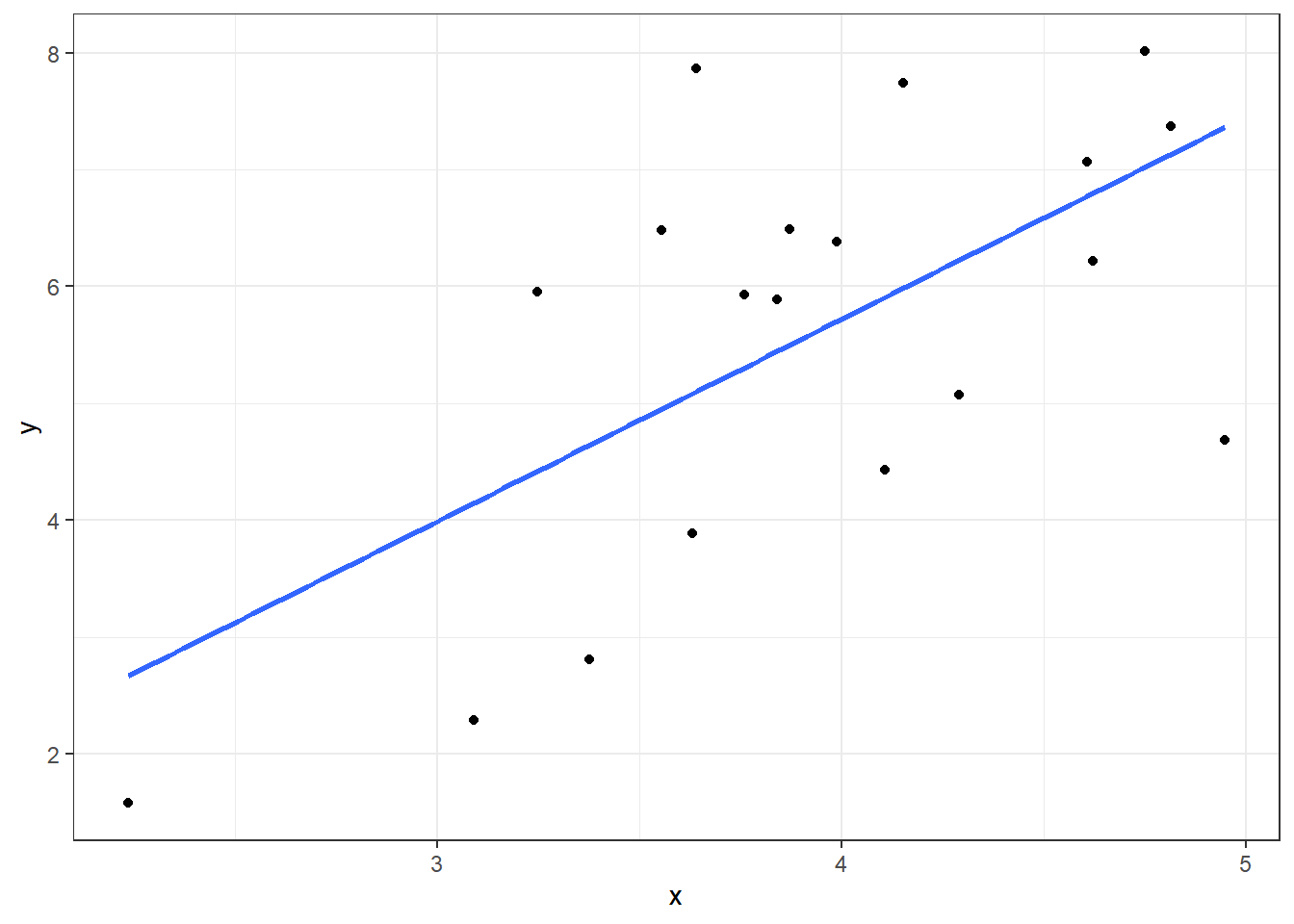
Garis Regresi Penjualan Motor (y) sebagai Fungsi dari Pendapatan per Kapita (x)

Gambar 1.2: Garis Regresi Penjualan Motor (y) sebagai Fungsi dari Pendapatan per Kapita (x)

Jika kita ekspresikan ke dalam persamaan, garis regresi yang memodelkan hubungan antara \(y\) dan \(x\) dapat kita tuliskan sebagai:

\[\begin{equation} y_i=\beta_0 + \beta_1x_i \tag{1.1} \end{equation}\]

Persamaan ini menyatakan bahwa \(y\) sebagai variabel respons adalah fungsi linier dari \(x\), variabel prediktor. \(\beta_0\) adalah intersep (intercept) yang menunjukkan nilai dari \(y\) jika \(x\) sama dengan nol. \(\beta_1\) adalah koefisien kemiringan garis (slope) yang menunjukkan berapa banyak \(y\) akan berubah jika \(x\) meningkat sebanyak satu unit.

Di dalam analisis regresi kita mencari nilai dugaan \(\hat \beta_0\) dan \(\hat \beta_1\) sehingga rata-rata jarak vertikal untuk setiap titik data pengamatan dengan nilai dugaannya secara kolektif paling kecil (Gambar 1.3). Dengan kata lain kita ingin menarik garis regresi dalam bidang x−y sedekat mungkin dengan persebaran titik-titik data sampel yang telah kita kumpulkan sehingga variasi yang tidak dapat dijelaskan oleh model menjadi minimum.

Salah satu cara untuk mendapatkan garis yang paling pas (line of best fit) yang sangat populer adalah melalui suatu prosedur formal yang disebut metode kuadrat terkecil/ordinary least squares (OLS). Sesuai namanya metode ini meminimalkan jumlah kuadrat kesalahan dari model.

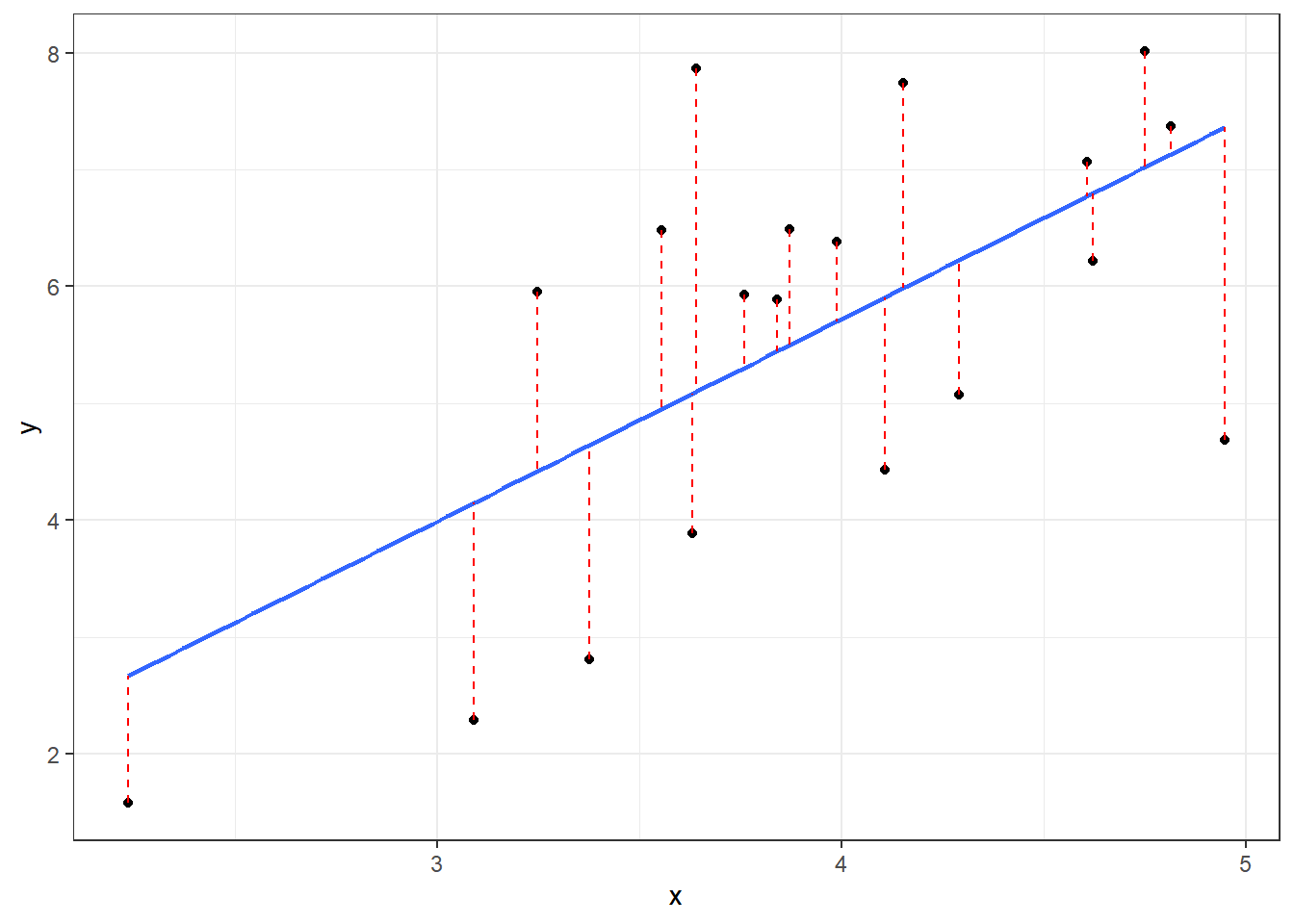
Mencari Garis Regresi dengan Metode Kuadrat Terkecil

Gambar 1.3: Mencari Garis Regresi dengan Metode Kuadrat Terkecil

Di dalam kasus penjualan motor, karena kita hanya menggunakan satu variabel prediktor dalam regresi sederhana, faktor lain selain pendapatan yang menyebabkan variasi pada penjualan motor kita masukkan sebagai faktor acak (random factor). Faktor acak ini secara visual ditunjukkan oleh panjang garis vertikal (warna merah putus-putus) antara titik data pengamatan dengan garis regresi atau nilai dugaan variabel respons (garis biru).

Faktor acak ini menunjukkan adanya variasi pada penjualan yang tidak dapat dijelaskan oleh model dan disimbolkan dengan \(\epsilon\). Maka persamaan garis regresi dapat kita tuliskan lagi sebagai:

\[\begin{equation} y_i=\beta_0 + \beta_1x_i + \epsilon_i \tag{1.2} \end{equation}\]

\(\epsilon_i\) dimasukkan ke dalam persamaan untuk mengakomodasi variasi dalam \(y\) yang tidak dapat dijelaskan oleh variabel \(x\). Faktor acak ini adalah istilah statistik yang mewakili fluktuasi acak, kesalahan pengukuran, atau dampak dari faktor-faktor diluar kendali peneliti (Faraway, 2016) yang menyebabkan nilai dugaan tidak sama dengan nilai aktual (error atau residu). Jadi \(\epsilon\) ini mewakili ketidakmampuan model untuk menjelaskan variasi yang terjadi pada variabel respons.

Setiap model pasti mengandung error, karena hubungan statistik tidak memiliki ketepatan seperti halnya fungsi matematika. Jadi ketika kita mencoba menjelaskan variabel \(y\) dengan menggunakan variabel \(x\) ini, kita menggunakan hubungan statistik: sebuah hubungan yang tidak eksak.

Bahkan, seandainya variabel-variabel lain ditambahkan ke dalam model, tetap akan ada variasi di dalam \(y\) yang tidak dapat dijelaskan oleh model. Variasi ini bisa karena bentuk fungsional yang tidak benar atau bisa juga karena semata-mata faktor kejadian yang tidak dapat diprediksi.

Sebuah model regresi linier yang sudah dikalibrasi paling pas dengan data sampel (the best fit), dapat digunakan untuk menjelaskan hubungan atau membuat prediksi dengan mencermati perbedaan (arah) dan intensitas perubahan (magnitud) dari variabel \(y\) pada nilai variabel \(x\) tertentu.

Analisis regresi menawarkan pendekatan yang masuk akal dengan mengenali pola-pola hubungan antar variabel: arah dan besar perubahan pada variabel respons dengan arah dan besar perubahan pada variabel prediktor dari model yang valid.

Dengan demikian persamaan regresi yang memodelkan hubungan statistik antar variabel terdiri dari dua komponen: komponen deterministik atau sinyal yaitu \(\beta_0 + \beta_1\) dan komponen acak yaitu \(\epsilon\). Kombinasi kedua komponen ini menjadikan persamaan regresi sebagai model non-eksak, yaitu bergantung pada bentuk-bentuk penjelasan probabilistik. Kita hanya mengasumsikan bahwa di dalam cakupan variabel yang dianalisis, terdapat tendensi variabel respons \(y\) untuk bervariasi secara sistematis dengan variabel prediktor \(x\).

Mayoritas analisis regresi yang baku menggunakan model regresi linier, yaitu mengasumsikan bahwa variabel respons dapat dituliskan sebagai kombinasi linier dari variabel-variabel prediktornya. Beberapa alasan mengapa model linier ini paling umum dipakai adalah (Rawlings, 1998): (1) model linier mudah dipahami; (2) beberapa model nonlinier secara instrinsik linier, sehingga bisa didekati dengan pendekatan linier.

Dalam banyak hal, jumlah variabel respons yang kita analisis bisa lebih dari satu atau \(p>1\), sehingga persamaan umum regresinya menjadi:

\[\begin{equation} y_i=\beta_0 + \beta_1x_{i1} + \beta_2x_{i2} + ... + \beta_px_{ip} + \epsilon_i \tag{1.3} \end{equation}\]

Model ini disebut sebagai model regresi linier berganda. Disebut berganda karena melibatkan lebih dari satu variabel prediktor. Contoh-contoh penerapannya:

  1. Seorang mahasiswa ingin menduga koefisien-koefisien dari sebuah model yang menghubungkan bobot tanaman vaskular-tanaman yang memiliki jaringan khusus yaitu xilem dan floem untuk mengangkut unsur hara, air dan mineral ke seluruh bagian tanaman-dengan kandungan unsur hara dalam tanah, jumlah air yang diterima dan jangka waktu tanaman terpapar sinar matahari.
  2. Kerja fisik (mengangkat, memutar, mendorong benda berat) tetap tidak dapat dihindari walaupun kita sudah mampu membuat alat-alat untuk membantu pekerjaan. Kadang pekerjaan itu harus kita lakukan dalam kondisi yang tidak ergonomis. Cedera tulang punggung seringkali ditemui pada pekerja di sektor ini. Seorang manajer produksi mungkin tertarik untuk mengurangi masalah cedera tulang belakang ini dengan menginvestigasi hubungan kepadatan mineral tulang belakang dengan usia, berat dan tinggi badan, jenis kelamin dan gaya hidup pekerja.
  3. Seorang analis ingin mengetahui tingkat kepuasan karyawan sebuah perusahaan terhadap pekerjaannya. Skor total kepuasan kerja karyawan dihitung dari penjumlahan skor-skor 20 pertanyaan dengan menggunakan 5 poin skala likert. Sedangkan prediktornya digunakan variabel demografi meliputi usia, jenis kelamin dan pendidikan terakhir karyawan.
  4. Di dalam teori konsumen, preferensi seorang konsumen terhadap suatu produk dipengaruhi oleh pengetahuan konsumen terhadap produk, emosi,word of mouth, faktor-faktor personal dan lingkungan.

1.2 Asumsi-Asumsi Model Linier

All models are wrong, but some are useful (Box, 1979). Seperti halnya metodologi statistik yang lain, analisis regresi linier dapat menjadi cara yang sangat efektif untuk memodelkan data sepanjang asumsi-asumsinya terpenuhi. Jika asumsinya tidak terpenuhi, metode kuadrat terkecil berpotensi memberikan hasil yang arahnya tidak tepat (misleading).

Setelah analisis regresi dilakukan, kita harus melakukan uji diagnostik: memastikan apakah model memenuhi asumsi-asumsi model linier. Uji diagnostik dapat dilakukan secara grafik maupun dengan uji formal.

Asumsi-asumsi regresi linier adalah:

  1. Linieritas data: hubungan antara prediktor \(x\) dengan respons \(y\) diasumsikan linier.
  2. Normalitas residu. error/residu diasumsikan terdistribusi secara normal.
  3. Homogenitas variansi residu: residu diasumsikan mempunyai variansi yang tetap (homoskedastisitas)
  4. Independensi residu.

Potensi-potensi tidak terpenuhinya asumsi model regresi adalah:

  1. Hubungan antara respons dengan prediktor tidak linier
  2. Heteroskedastisitas: variansi residu tidak tetap.
  3. Adanya nilai-nilai yang “berpengaruh” besar yang berasal dari (a) nilai pencilan (outlier) yaitu nilai-nilai ekstrim pada variabel respons; (b) high-leverage points: nilai-nilai ekstrim pada variabel prediktor.

Uji hipotesis, interval dan prediksi didasarkan atas kepercayaan bahwa asumsi-asumsi model regresi dipenuhi. Jadi penting sekali untuk melakukan pengecekan terhadap asumsi-asumsi ini. Jika asumsi-asumsi dipenuhi, berbagai bentuk inferensi seperti prediksi, kontrol, ekstraksi informasi, penemuan pengetahuan dan evaluasi risiko dapat dilakukan dengan kerangka argumen deduktif sesuai dengan model yang dibangun.

1.3 Uji Signifikansi

Salah satu fungsi dari regresi linier adalah untuk estimasi kondisi populasi. Kita mengamati dan mengumpulkan data sampel, tetapi kita ingin mengetahui apakah data sampel yang kita miliki juga menerangkan sesuatu tentang populasi dimana data ini diambil. Dengan kata lain kita ingin mengetahui apakah hasil dari analisis data sampel dapat digeneralisasi ke populasi dengan uji signifikansi.

Uji signifikansi dapat dilakukan jika asumsi-asumsi model regresi telah dipenuhi. Uji-uji signifikansi itu antara lain:

  1. Uji t: digunakan untuk mengetahui apakah koefisien-koefisien regresi secara statistik berbeda secara signifikan (statistically-significantly) dari nol.

  2. Uji F: jika uji t digunakan untuk menguji hanya satu koefisien, uji F digunakan untuk menguji lebih dari satu koefisien secara serempak.

1.4 Langkah-langkah Melakukan Analisis Regresi

Berdasarkan uraian sebelumnya, secara umum langkah-langkah dalam melakukan analisis regresi adalah sebagai berikut:

  1. Menentukan variabel respons \(y\) yang akan kita pelajari atau buat modelnya.
  2. Menentukan sejumlah variabel prediktor yang kita anggap berguna di dalam menjelaskan variabel respons. Secara fisik atau teori variabel prediktor yang dipilih memang berkaitan dengan variabel respons.
  3. Mengumpulkan data (sampel) yang dapat digunakan untuk membuat model.
  4. Mengestimasi model.
  5. Cek kecukupan model/uji diagnostik (jika hasilnya kurang memuaskan, kembali ke tahap 1).
  6. Mengaplikasikan hasil analisis regresi.

1.5 Penggunaan Komputer

Jika diperhatikan langkah-langkah untuk melakukan analisis regresi pada 1.3, membangun model regresi merupakan sebuah proses iteratif. Dimulai dengan kajian teori yang berhubungan topik yang sedang diteliti dan ketersediaan data untuk menentukan variabel respons dan variabel eksplanatori untuk membangun model awal.

Salah satu pertimbangan penting di dalam memilih variabel prediktor adalah apakah variabel tersebut dapat mengurangi variasi dalam variabel respons. Pertimbangan lain adalah seberapa mudah, murah dan akurat data variabel itu bisa diperoleh dibandingkan calon variabel prediktor yang lain. Pemilihan ini harus cermat karena bagaimanapun model adalah sebuah penyederhanaan dari realitas yang lebih kompleks, sehingga sebaiknya beberapa prediktor saja dimasukkan ke dalam model.

Menampilkan data dalam grafik atau diagram pencar seringkali sangat berguna untuk spesifikasi model awal. Setelah itu parameter-parameter model diestimasi. Setelah itu kecukupan model dievaluasi yang meliputi mencari kemungkinan terjadi kesalahan spesifikasi model, kemungkinan tidak memasukkan variabel penting atau memasukkan variabel yang tidak perlu, menemukan data pencilan (outlier).

Kecukupan dan kecocokan model harus dicek karena menentukan apakah model yang dibuat dapat dipakai atau tidak. Hasil dari cek kecukupan mungkin mengindikasikan apakah model yang dibuat cukup masuk akal atau perlu dimodifikasi. Di dalam uji kecukupan terutama yang perlu dicek adalah residu sebagai realisasi dari kesalahan model \(\epsilon\).

Jika model tidak cukup memenuhi, maka perlu dilakukan tindakan perbaikan dan pendugaan paramater diulang lagi. Proses ini mungkin perlu diulang beberapa kali sampai diperoleh model yang memuaskan. Selanjutnya dilakukan validasi untuk memastikan bahwa model dapat diterima di dalam tahap akhir penerapannya.

Dengan demikian, analisis regresi seringkali melibatkan banyak penghitungan, apalagi jika jumlah sampelnya besar dan variabel prediktornya banyak. Untuk membantu mempercepat proses ini kita menggunakan program komputer.

Program komputer yang bagus adalah alat yang diperlukan dalam proses membangun model. Tetapi program komputer saja belum cukup. Analisis regresi memerlukan seni dan inteligensia dalam penggunaan komputer. Analis harus belajar bagaimana menginterpretasikan output komputer dan mengintegrasikan informasi yang didapat dengan model-model yang akan dibuat selanjutnya.

Berbagai program statistik seperti SPSS, Stata, Minitab, Eviews, SAS, JMP, R, dan lain-lain dapat melakukan penghitungan regresi secara cepat dengan hasil yang kurang lebih sama. Di buku ini saya menggunakan software R (R Core Team, 2021) untuk membuat grafik maupun penghitungan regresinya.