2 Regresi Linier Sederhana

Tedy Herlambang

Bab ini akan membahas regresi linier sederhana. Istilah regresi sederhana tidak merujuk pada kenaifan penelitiannya tetapi merujuk pada model yang hanya terdiri dari satu variabel respons dan satu variabel prediktor.

Situasi ini sering terjadi pada penelitian sains. Misalnya seorang peneliti ingin memprediksi laju reaksi kimia karena perubahan temperatur, atau ingin mengetahui hubungan antara perubahan diet dengan tingkat kolesterol pada seseorang. Jika dapat diasumsikan bahwa variabel-variabel ini terhubung secara linier, kita dapat menggunakan regresi linier sederhana untuk mengkuantifikasi hubungan ini.

Analisis regresi digunakan ketika solusi eksak tidak tersedia, dalam arti kita tidak akan dapat menemukan nilai tunggal yang dapat mencakup secara lengkap hubungan antara variabel respons dengan prediktornya. Sehingga disini kita mencoba memprediksi setepat mungkin variabel respons atau memprediksi dengan kesalahan terkecil.

Untuk mencapai tujuan ini, kita menganalisis pola-pola variabilitas pada variabel respons dan mencoba melihat apakah variabilitas ini dapat diprediksi dari variabilitas prediktornya.

2.1 Model Regresi Linier Sederhana

Model regresi linier sederhana dapat dituliskan sebagai berikut:

\[\begin{equation} y_i=\beta_0 + \beta_1x_i+ \epsilon_i \tag{2.1} \end{equation}\]

Regresi sederhana mengindikasikan hanya ada satu variabel prediktor x untuk menduga variabel respons y. Linier disini diartikan modelnya linier pada parameternya dalam hal ini \(\beta_0\) dan \(\beta_1\). Jadi model \(y_i = \beta_0 + \beta_1{x_i}^2 + \epsilon_i\) adalah linier pada \(\beta_0\) dan \(\beta_1\), sementara model \(y_i = \beta_0 + e^{\beta_ix_i} + \epsilon_i\) tidak linier.

Misalkan kita memiliki pasangan-pasangan data sampel sebanyak n yang diambil secara acak dari populasi yang lebih besar \((x_1,y_1), (x_2,y_2), ⋯, (x_n,y_n)\). Tujuan dari analisis regresi linier adalah menemukan model terbaik yaitu menemukan nilai \(\beta_0\) and \(\beta_1\) yang menghasilkan garis paling cocok dengan titik-titik data yang kita punyai.

Dengan kata lain tujuan dari analisis regresi adalah mengestimasi koefisien regresi untuk variabel prediktor sehingga didapatkan nilai dugaan variabel respons sedekat mungkin nilainya dengan nilai pengamatan aktualnya.

Di dalam analisis regresi, model terbaik ditunjukkan oleh garis lurus yang menghubungkan rata-rata variabel prediktor dengan variabel respons sedemikian rupa sehingga jumlah kuadrat kesalahan (jarak vertikal antara titik-titik data pengamatan aktual \(y_i\) dengan nilai dugaannya \(\hat y_i\)) minimal.

Untuk memperoleh nilai dugaan \(\beta_0\) dan \(\beta_1\) yang paling cocok, kita menggunakan metode kuadrat terkecil (method of least squares). Dengan pendekatan kuadrat terkecil, kita mencari nilai dugaan \(\beta_0\) dan \(\beta_1\) yang meminimalkan jumlah kuadrat residu/kesalahan (\(y_i-\hat y_i\)).

2.1.1 Kasus 1: Penjualan Motor dan Pertumbuhan Pendapatan Perkapita

Kita akan melanjutkan kasus hubungan antara penjualan motor dengan pendapatan pada Bab 1 sebelumnya sebagai ilustrasi regresi linier sederhana. Data dapat diunduh di sini. Langkah awal untuk melihat bagaimana hubungan antar variabel adalah membuat diagram pencar.

Plot sangat penting di dalam regresi. Pemeriksaan diagram pencar secara teliti harus mendahului penghitungan regresi. Diagram pencar dapat mengindikasikan apakah model regresi yang diinginkan mungkin masuk akal atau tidak. Kesepakatan dalam membuat diagram pencar, variabel \(x\) sebagai variabel penjelas diplot pada sumbu horisontal. Varibel \(y\) sebagai variabel respons diplot pada sumbu vertikal.

Untuk membuat diagram pencar, hal pertama yang harus dilakukan adalah memasukkan data ke dalam R, mengecek apakah data yang kita masukkan sudah betul dan memanggil package yang relevan dengan model yang akan dibuat.

# memanggil data yang disimpan dalam bentuk teks ke dalam R
PJMotor <- read.delim("PJMotor.txt") 
PJMotor <- as.data.frame(PJMotor)
# attach(PJMotor)

# untuk melihat beberapa baris data teratas
head(PJMotor)

##   Tahun        y        x
## 1  2001 1.575822 2.235180
## 2  2002 2.287706 3.090636
## 3  2003 2.809896 3.376533
## 4  2004 3.887678 3.630909
## 5  2005 5.074186 4.289591
## 6  2006 4.428274 4.107514

# untuk melihat beberapa baris data terakhir
tail(PJMotor)

##    Tahun        y        x
## 14  2014 7.867195 3.639072
## 15  2015 6.480155 3.555062
## 16  2016 5.931285 3.758837
## 17  2017 5.886103 3.841197
## 18  2018 6.383108 3.987825
## 19  2019 6.487460 3.871444

Data yang kita masukkan kelihatan seperti yang diharapkan. Variabel penjualan dan pendapatan semua dibaca sebagai angka (numeric data type). Selanjutnya kita akan lihat struktur dan ringkasan persebaran datanya.

# melihat struktur data
str(PJMotor)

## 'data.frame':    19 obs. of  3 variables:
##  $ Tahun: int  2001 2002 2003 2004 2005 2006 2007 2008 2009 2010 ...
##  $ y    : num  1.58 2.29 2.81 3.89 5.07 ...
##  $ x    : num  2.24 3.09 3.38 3.63 4.29 ...

Hasil fungsi str() menunjukkan bahwa data ini adalah data time series terdiri dari tiga kolom yaitu penjualan motor (y), pertumbuhan pendapatan per kapita (x) dan tahun selama 19 tahun dari 2001-2019.

# melihat ringkasan data kecuali data tahun
summary(subset(PJMotor, select = c(y,x)))

##        y               x        
##  Min.   :1.576   Min.   :2.235  
##  1st Qu.:4.558   1st Qu.:3.593  
##  Median :5.952   Median :3.871  
##  Mean   :5.587   Mean   :3.922  
##  3rd Qu.:6.776   3rd Qu.:4.448  
##  Max.   :8.013   Max.   :4.946

Selanjutnya kita cek normalitas data, korelasi dan diagram pencar antara pasangan data \(y\) dengan \(x\) seperti yang ditunjukkan pada Gambar 2.1 dengan menggunakan paket GGally.

library (GGally)

## Registered S3 method overwritten by 'GGally':
##   method from   
##   +.gg   ggplot2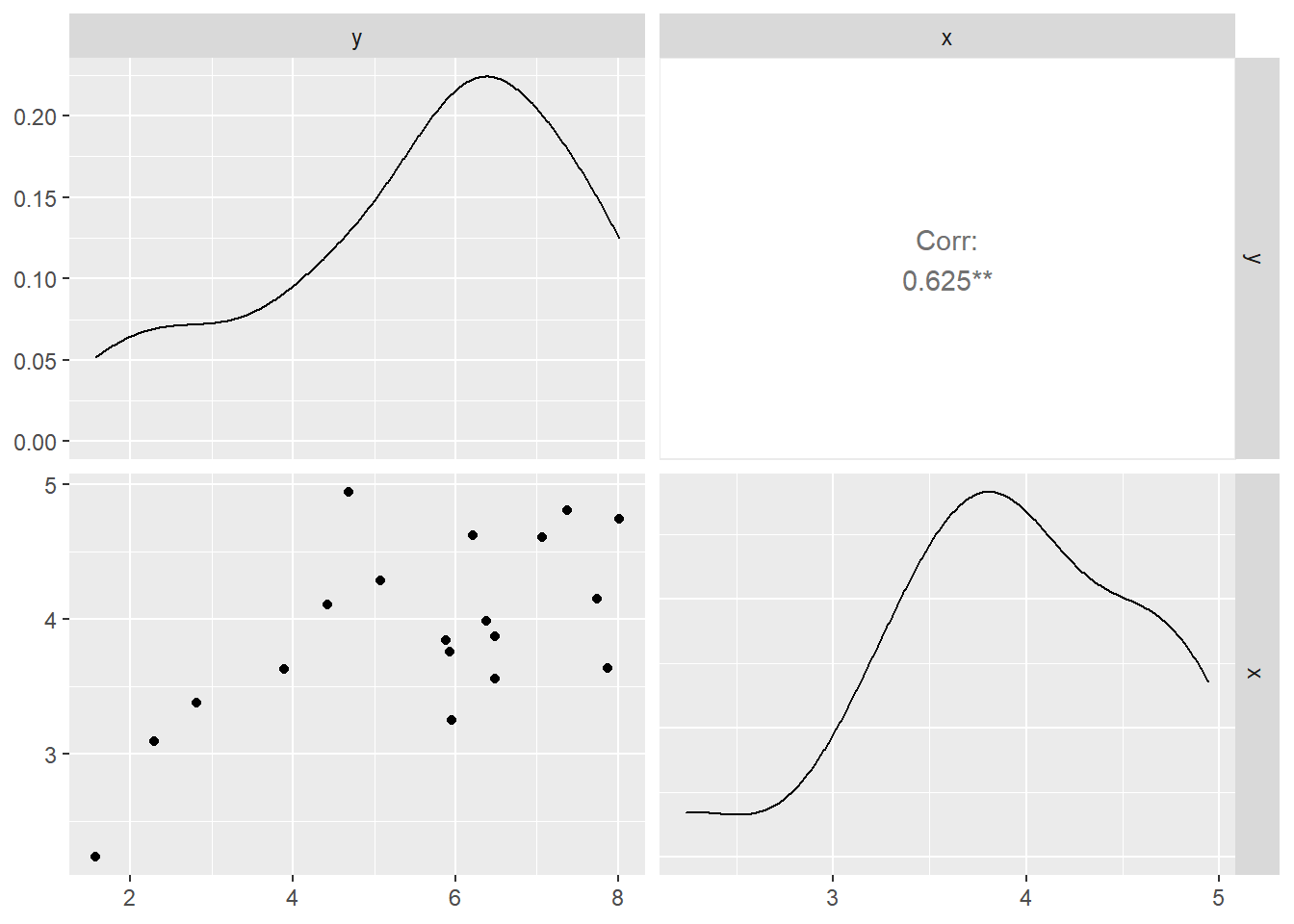

GGally::ggpairs(subset(PJMotor, select = c(y,x)))

Gambar 2.1: Plot Pasangan Data Penjualan dan Pendapatan

Pada diagonal, kita melihat distribusi data \(y\) dan \(x\): data kedua variabel menceng ke kiri (skewed left). Di atas diagonal ditunjukkan nilai korelasi antara \(y\) dan \(x\) yaitu sebesar=0.625. Koefisisen korelasi nilainya antara −1 (berkorelasi negatif sempurna) melalui 0 (tidak ada korelasi) sampai +1 (berkorelasi positif sempurna). Korelasi antara penjualan dan pendapatan disini positif cukup kuat dan signifikan. Grafik dibawah diagonal menunjukkan diagram pencar antara pasangan data \(y\) dengan \(x\) seperti yang sudah kita bahas sebelumnya di Bab 1.

Di dalam R model regresi linier sederhana dapat diperoleh dengan perintah lm(y~x). Tanda ~ dapat diartikan \(y\) dijelaskan oleh \(x\) atau \(y\) fungsi dari \(x\). Fungsi ini mengestimasi koefisien regresi model linier dengan metode kuadrat terkecil (the least squares method).

Semisal modelnya kita beri nama model penjualan motor (mpm), yang memodelkan hubungan antara penjualan motor (\(y\)) dengan pertumbuhan pendapatan (\(x\)), maka model ini dapat diperoleh dengan perintah:

mpm <- lm(y ~ x) 
# Perintah ini sama dengan $y = β_0 + β_1x$
# Intersep secara default diestimasi. 
# Bandingkan dengan perintah untuk mendapatkan diagram pencar.

Kita kemudian menggunakan perintah summary() untuk menampilkan luarannya. Hasilnya adalah sebagai berikut:

# perintah summary() untuk mengekstrak hasil regresi
summary (mpm)

## 
## Call:
## lm(formula = y ~ x)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -2.6738 -1.1721  0.2916  0.9911  2.7707 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)   
## (Intercept)   -1.210      2.088  -0.579  0.56999   
## x              1.733      0.525   3.301  0.00422 **
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 1.515 on 17 degrees of freedom
## Multiple R-squared:  0.3906, Adjusted R-squared:  0.3547 
## F-statistic: 10.89 on 1 and 17 DF,  p-value: 0.004224

Persamaan regresinya dapat diringkas sebagai \(\hat {penjualan}=-1.21+1.73*pendapatan\). Nilai dugaan intersep garis regresi \(\hat \beta_0\) = -1.210 (SE= 2.088), p-value = 0.57 (tidak signifikan). Nilai -1,21 menunjukkan dugaan penjualan sepeda motor (y dalam juta unit) jika pertumbuhan pendapatan per kapita sebesar 0 persen. Angka penjualan tidak mungkin negatif, paling rendah adalah 0. Jadi dalam kasus ini, nilai intersep dari model yang kita duga tidak mempunyai interpretasi yang berarti. Jadi intersep di dalam sebuah persamaan kadang-kadang mempunyai interpretasi yang berarti kadang juga tidak seperti dalam kasus kita ini.

Sedangkan nilai dugaan variabel prediktor pendapatan \(\hat \beta_1\) = 1.733 (SE = 0.525) dan p-valuenya (menguji hipotesis nol bahwa \(\beta_1\) = 0) kecil (signifikan), konsisten dengan bukti persebaran data yang cenderung linier. Jadi 1.733 adalah nilai kemiringan garis regresi yang menunjukkan untuk setiap perubahan pertumbuhan pendapatan per kapita sebesar 1%, berkaitan dengan perubahan penjualan motor sebesar 1.73 juta unit. Jika terjadi kenaikan pertumbuhan pendapatan per kapita sebesar 1 persen, ini berkaitan dengan peningkatan penjualan motor sebanyak 1.73 juta unit.

Output lain yang penting dari perintah summary() adalah koefisisen determinasi (\(R^2\)) sebesar 0.39. Ini berarti pendapatan dapat menjelaskan sebesar 39% variasi pada data penjualan motor. Dengan kata lain jika kita ingin menjelaskan mengapa penjualan motor naik turun, maka kita bisa melihat variasi pada pertumbuhan pendapatan. Tentu saja ada faktor lain yang menjelaskan fluktuasi penjualan motor. Tetapi karena model kita hanya memasukkan pendapatan sebagai variabel eksplanatori, maka cukup masuk akal jika model ini hanya menjelaskan sebanyak 39%. Artinya terdapat 61% variasi pada penjualan motor yang tidak bisa dijelaskan oleh pendapatan perkapita saja.

Selang kepercayaan batas atas dan batas bawah (95% defaultnya) untuk nilai dugaan koefisien dapat diperoleh dengan perintah confint().

# perintah menampilkan selang kepercayaan
confint(mpm)

##                 2.5 %   97.5 %
## (Intercept) -5.615467 3.196075
## x            0.625206 2.840601

Terlihat bahwa selang kepercayaan untuk intersep meliputi angka 0 sehingga kita simpulkan bahwa intersep disini tidak signifikan. Sedangkan untuk prediktor pertumbuhan pendapatan kita 95 yakin bahwa selang antara (0.63,2.84) meliputi perubahan penjualan motor yang sebenarnya jika terjadi perubahan pertumbuhan pendapatan per kapita sebesar 1%. Tetapi keyakinan kita akan hasil ini hanya sekuat bukti-bukti yang kita miliki bahwa data kita memenuhi asumsi-asumsi model linier yang akan kita bahas di bagian selanjutnya.

2.1.1.1 Residu

Selisih antara nilai data aktual penjualan motor \(y_i\) dengan nilai dugaannya \(\hat y_i\) pada saat pendapatan \(x = x_i\) disebut residu. Nilai residu mencerminkan kegagalan garis regresi yang diestimasi untuk memodelkan pasangan data tersebut. Bagaimana nilai residu diperoleh secara detil?

\(\hat \beta_0\) dan \(\hat \beta_1\) adalah nilai-nilai koefisien garis regresi dengan menggunakan data sampel sebanyak 19 tahun \((x_1, y_1),(x_2, y_2), . . . , (x_{19}, y_{19})\). Untuk setiap pertumbuhan pendapatan per tahun sebesar \(x\), nilai dugaaan penjualan motornya adalah sebesar \(\hat y = \hat \beta_0 + \hat \beta_1x\). Untuk setiap pertumbuhan pendapatan sebesar \(x_i\), dimana \(i = 1, 2, . . . , 19\), nilai selisih antara \(y_i−\hat y_i = y_i − (\hat \beta_0 + \hat \beta_1x_i)\) disebut residu.

Nilai residu ini dapat diperoleh dengan menggunakan perintah augment() dari broom package. Misalkan residu dari perintah augment() kita sebut sebagai uji.diagnostik (dibahas secara lebih lengkap di Bab 4):

# menambahkan nilai-nilai dugaan dan residu
# library perlu dipanggil jika belum dipanggil sebelumnya
library("broom") 
uji.diagnostik <- augment(mpm)
head(uji.diagnostik)

## # A tibble: 6 × 8
##       y     x .fitted .resid   .hat .sigma .cooksd .std.resid
##   <dbl> <dbl>   <dbl>  <dbl>  <dbl>  <dbl>   <dbl>      <dbl>
## 1  1.58  2.24    2.66  -1.09 0.394    1.52  0.277      -0.922
## 2  2.29  3.09    4.15  -1.86 0.136    1.48  0.136      -1.32 
## 3  2.81  3.38    4.64  -1.83 0.0883   1.49  0.0776     -1.27 
## 4  3.89  3.63    5.08  -1.19 0.0628   1.53  0.0222     -0.814
## 5  5.07  4.29    6.22  -1.15 0.0689   1.53  0.0228     -0.786
## 6  4.43  4.11    5.91  -1.48 0.0568   1.51  0.0304     -1.01

Kolom-kolom pada tabel diatas menunjukkan

x: pertumbuhan pendapatan per kapita
y: penjualan motor aktual
.fitted: nilai dugaan penjualan motor
.resid: nilai residu (penjualan motor aktual-nilai dugaan penjualan motor)

Kode berikut memplot nilai residu (warna merah) yaitu selisih antara nilai pengamatan aktual dengan nilai dugaan. Setiap garis vertikal warna merah menunjukkan nilai residu antara data penjualan motor aktual dengan nilai dugaannya.

# library tidak perlu dipanggil lagi jika sudah dipanggil sebelumnya
library(ggplot2) 
library(ggpmisc)
rumus <- y ~ x
ggplot(uji.diagnostik, aes(x, y)) +
  geom_point() +
  stat_smooth(method = "lm", se = FALSE, formula = rumus, 
  size = 0.8) + geom_segment(aes(xend = x, yend = .fitted), 
  color = "red", size = 0.4,linetype = "dashed") + theme_bw()+
  stat_poly_eq(formula = rumus,
                eq.with.lhs = "italic(hat(y))~`=`~",
                aes(label = paste(..eq.label.., ..rr.label.., 
                sep = "~~~")), parse = TRUE)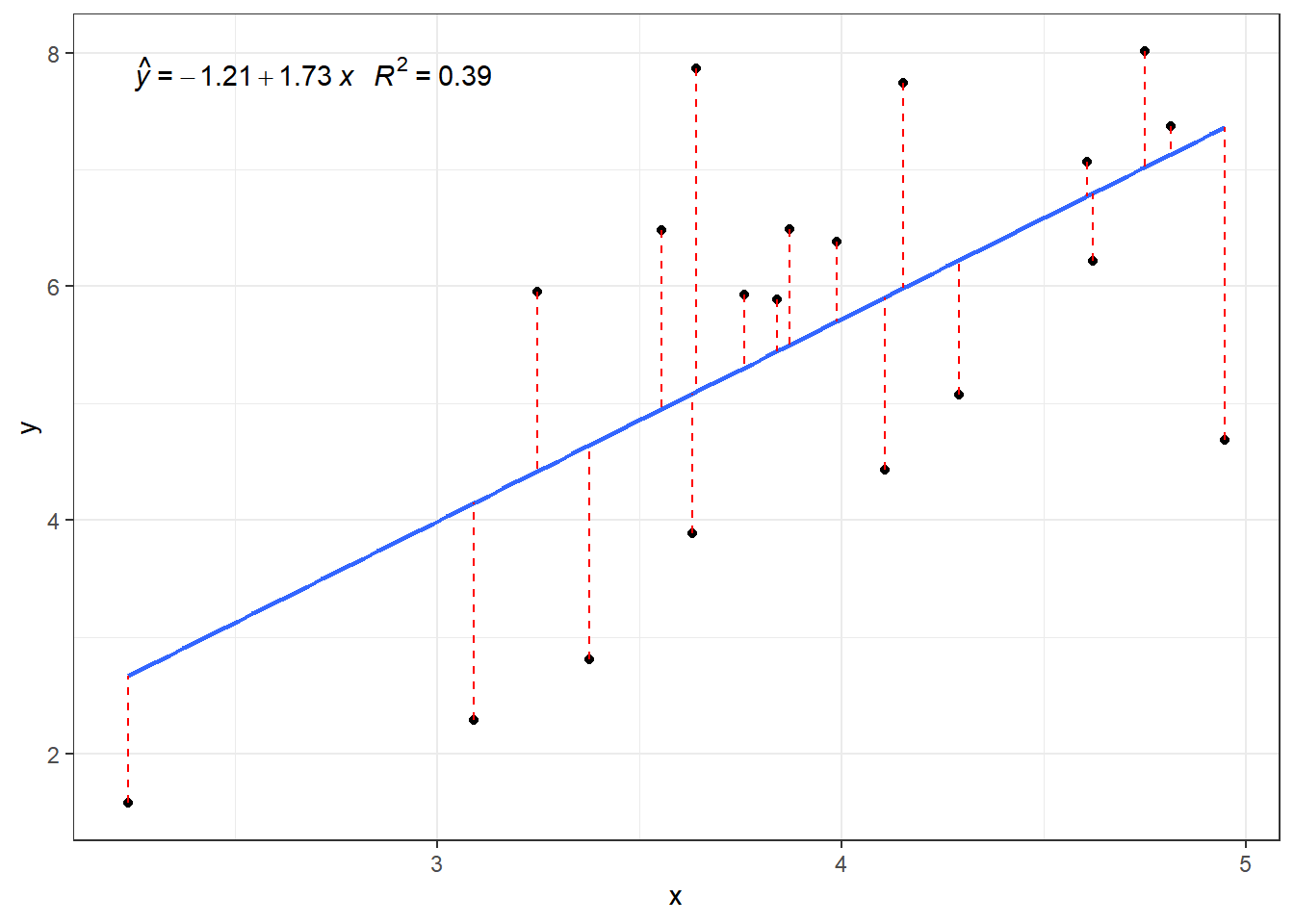

Gambar 2.2: Ilustrasi Geometris OLS. Jarak antara Pengamatan dengan Garis Regresi Sepanjang Sumbu y

2.1.1.2 Uji Diagnostik Regresi

Regresi diagnostik merujuk pada sekelompok teknik untuk mendeteksi masalah di dalam regresi baik yang berhubungan dengan modelnya atau datanya (Rawlings, 1998). Iregularitas di dalam data atau kesalahan spesifikasi hubungan antara variabel prediktor dengan respons dapat menghasilkan model yang tidak akurat. Bisa juga kita menyimpulkan tidak ada hubungan antara sebuah prediktor dengan variabel respon, padahal mereka ada hubungan atau sebaliknya. Dampak lain yang mungkin terjadi adalah kita secara nyata keliru membuat prediksi ketika model diterapkan di dunia nyata.

Dengan demikian, setelah melakukan analisis regresi kita harus mempertimbangkan bahwa validitas dari model yang diperoleh meragukan dan memastikan bahwa model memenuhi asumsi-asumsinya. Hal ini penting karena pada saat kita membuat prediksi dan inferensi statistik tentang populasi dari mana sampel diambil, kita membuat beberapa asumsi yang bisa sesuai atau tidak sesuai dengan data sampel yang kita miliki.

Model yang tidak memenuhi asumsi-asumsi ini berpotensi berdampak serius. Pelanggaran nyata-nyata asumsi dapat menghasilkan model yang tidak stabil dalam arti jika kita menggunakan data sampel yang berbeda kita bisa menghasilkan model yang benar-banar berbeda dan kesimpulan yang berlawanan.

Langkah pertama dalam diagnostik regresi adalah menginspeksi signifikansi koefisien regresi dan nilai \(R^2\) yang dapat menunjukkan apakah model linier cocok dengan data. Koefisien determinasi \(R^2\) sebagai ukuran kasar tentang kecocokan data tidak seharusnya dijadikan sebagai satu-satunya ukuran untuk menentukan kecocokan model. Kita biasanya tidak dapat mendeteksi pelanggaran asumsi dengan menggunakan uji statistik yang standar saja seperti uji \(t\), \(F\) atau melihat nilai \(R^2\). Uji-uji ini hanya menunjukkan kondisi “global” dari model regresi dan tidak memastikan kecukupan pemenuhan asumsi model.

Bagian ini akan menampilkan beberapa metode yang berguna untuk mendiagnosa pelanggaran-pelanggan asumsi-asumsi dasar model regresi linier. Sebagai review tentang asumsi-asumsi yang harus dipenuhi di dalam analisis regresi agar koefisien regresi bisa kita interpretasi dengan tepat adalah:

Linieritas: variabel respons berhubungan secara linier dengan variabel eksplanatori.
Normalitas: untuk setiap nilai variabel prediktor yang tetap, variabel respons terdistribusi secara normal.
Homoskedastisitas: varians dari variabel respons konstan pada berbagai nilai variabel eksplanatori.
Independen: nilai \(y_i\) independen satu sama lain.

Pelanggaran terhadap asumsi-asumsi ini akan mengakibatkan uji signifikansi statistik dan selang kepercayaan tidak akurat. Metode diagnostik ini terutama didasarkan pada analisis nilai-nilai residu. Uji diagnostik secara langsung pada variabel respons \(y\) dengan memplotnya biasanya tidak terlalu berguna di dalam analisis regresi karena nilai pengamatan variabel respons adalah fungsi dari variabel prediktor.

Analisis residu yang akan kita bahas ini tidak hanya bisa diterapkan pada model regresi sederhana tetapi juga untuk model regresi yang lebih kompleks. Walaupun analisis residu menggunakan grafik disini hanya informal, tetapi dalam berbagai hal sudah cukup untuk melihat kecocokan model dengan data.

Beberapa plot residu berikut akan digunakan untuk tujuan ini:

Plot nilai residu terhadap nilai dugaan(fitted values) untuk uji linieritas.
Plot residu terhadap garis normal: uji normalitas
Homogenitas varians
Pencilan (outliers) dan high leverage points (cook’s distance)

Keempat plot di atas dapat diperoleh sekaligus dengan perintah plot(nama-model), dalam kasus penjualan motor maka perintahnya adalah plot(mpm). Sebelumnya bidang kita bagi menjadi 2 kolom dan 2 baris. Perintah ini akan menghasilkan empat plot seperti yang ditunjukkan oleh Gambar 2.3.

par(mfrow=c(2,2)) # digunakan untuk menggabungkan 4 plot sekaligus kedalam bidang 2 x 2 
plot(mpm)

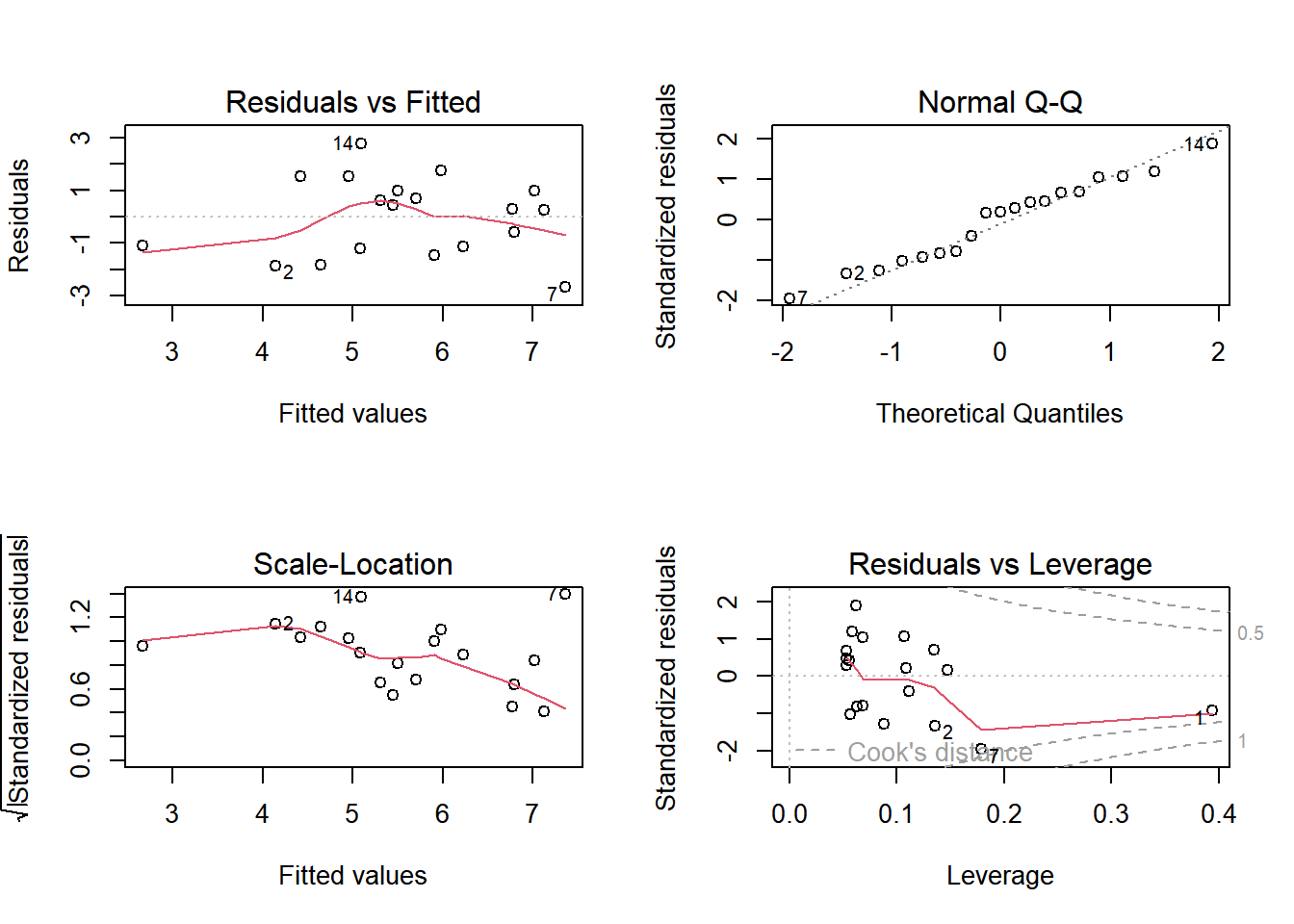
Gambar 2.3: Plot Residu

Membacanya dari kiri atas searah jarum jam. No 1 (kiri atas) merupakan plot antara nilai dugaan (fitted values) dengan residu. No 2 (kanan atas) menunjukkan plot normalitas nilai residu. No 3 (kanan bawah) adalah plot Pencilan (outliers) dan high leverage points (cook’s distance). No 4 (kiri bawah) adalah plot untuk uji homogenitas.

Gambar 2.3 kiri atas adalah plot residu dengan nilai dugaan. Plot ini memvisualkan pola-pola pada residu yang dapat mengindikasikan apakah fungsi persamaan linier cocok untuk data atau tidak. Linieritas fungsi regresi juga bisa dipelajari dari diagram pencar, tetapi diagram pencar tidak seefektif plot residu untuk melihat linieritas.

Persamaan yang digunakan untuk menghubungkan antara nilai dugaan variabel respons (\(y\)) dengan berbagai nilai variabel eksplanatori (\(x\)) menjelaskan pola sebenarnya dari data. Dengan kata lain, kita menggunakan persamaan garis lurus karena kita mengasumsikan secara kasar pola data benar-benar linier.

Penggunaan persamaan yang salah (seperti pemakaian garis lurus untuk data yang berpola kurva) dampaknya sangat serius. Nilai dugaan akan bias yaitu secara sistematis nilai dugaan keliru memprediksi pola sebenarnya dari nilai \(y\) dihubungkan dengan \(x\).

Idealnya, hasil plot antara residu dengan nilai dugaan \(\hat y\) tidak menunjukkan pola-pola tertentu, tidak ada hubungan sistematis antara residu dengan nilai dugaan. Garis merah harus mendekati horisontal pada angka nol. Hasil plot antara residu dengan nilai dugaan yang berpola kurva mengindikasikan bahwa jenis persamaan yang dipakai tidak tepat. Kehadiran pola-pola pada plot kiri mungkin mengindikasikan aspek lain dari model linier yang dipakai: mungkin model linier tidak pas, atau ada variabel prediktor yang tidak dimasukkan ke model. Di dalam kasus penjualan motor, tidak terdapat indikasi pengklasteran nilai residu, sehingga memenuhi asumsi linieritas.

Gambar 2.3 kanan atas adalah plot probabilitas normal nilai-nilai residu. Jika residu berasal dari distribusi normal, maka titik-titik persebaran akan berada dekat disekitar garis. Histogram yang berbentuk genta dapat dijadikan patokan normalitas nilai residu. Kesulitannya adalah bentuk histogram sulit dinilai kecuali jumlah data yang dimiliki besar. Oleh karena itu digunakan plot nilai residu terstandardisasi terhadap nilai dugaan teoritis data yang berasal dari populasi normal. Berdasarkan hasil plot, maka dapat disimpulkan data penjualan motor terdistribusi secara normal.

Gambar 2.3 kiri bawah adalah plot untuk melihat homogenitas varians. Homogenitas artinya residu memiliki nilai teoritis varians \(\sigma^2\) yang sama, tidak tergantung pada nilai \(x\) dan nilai dugaan \(\hat y\). Untuk sebuah garis lurus, ini berarti bahwa variasi vertikal dari titik-titik data disekitar garis regresi mempunyai magnitud yang sama.

Konsekuensi dari pelanggaran asumsi varians yang konstan tidak begitu serius, yaitu nilai dugaan kurang efisien dan nilai dugaan varians kesalahan tidak valid. Konsekuensi utama dari pelanggaran asumsi ini dimana varians tidak sama pada setiap nilai \(x\) adalah selang prediksi untuk nilai-nilai \(y\) akan keliru. Dampak dari pelanggaran asumsi ini pada validitas uji-\(t\), uji-\(F\) kecil karena pada umumnya inferensi regresi cukup tahan terhadap masalah varians.

Jika data yang memenuhi asumsi varians konstan, maka titik-titik pada grafik Scale-Location harus tersebar secara acak disekitar garis horisontal. Pada kasus regresi penjualan motor, kita memenuhi asumsi ini.

Gambar 2.3 kanan bawah adalah plot antara nilai residu dengan pengungkit (Residuals vs. Leverage). Plot ini cukup sulit untuk mengartikannya. Bahkan menurut Kabacoff (2022) plot ini tidak terlalu berguna.

Untuk menutup bab ini kita bisa tarik beberapa kesimpulan. Model regresi linier mengasumsikan garis linier dapat mewakili data yang dianalisis dan residu bersifat independen, terdistribusi normal dan memiliki varians yang konstan (homoskedastik). Sedangkan asumsi independensi data tergantung pada bagaimana data dikumpulkan.

Uji linieritas, normalitas dan homoskedastisitas memerlukan perhitungan nilai dugaan \(\hat y\) dan nilai residu \(e\). Nilai dugaan adalah nilai variabel respons yang diduga berdasarkan persamaan garis regresi untuk setiap nilai variabel prediktor \(x\). Nilai residu adalah selisih antara nilai pengamatan variabel respons dengan nilai dugaannya. Nilai-nilai residu yang jauh dari nol adalah pengamatan yang tidak diwakili dengan baik oleh garis regresi.

Uji statistik bisa dilakukan untuk menentukan apakah asumsi linieritas, normalitas dan homoskedastisitas dipenuhi. Pada umumnya uji diagnostik dilakukan dengan melihat 4 plot nilai residu yang bisa diperoleh dengan perintah plot(nama-model). Menurut Ogle (2016) sebenarnya uji diagnostik cukup dengan melihat dua plot saja yaitu no 1 dan 2 kita dapat mengetahui apakah asumsi model OLS dipenuhi. Terutama untuk plot no 4 cukup sulit untuk menginterpretasikannya, sehingga plot ini bahkan dianggap tidak terlalu berguna oleh (Kabacoff, 2022).

1 Pendahuluan

3 Regresi Linier Berganda